le plus grand nombre

Quel est le plus grand nombre? Qu'est-ce que Google? Qu'appelle-t-on grands nombres? Qu'est-ce que l'infini?

Quel est le plus grand nombre?

Il n'y a pas le plus grand nombre! Pourquoi? Bien, 1 000 000 000 (1 milliard) ne peut pas être le plus grand nombre, Parce que 1 milliard + 1 est plus gros – mais c'est vrai pour n'importe quel nombre que vous choisissez. Vous pouvez choisir n'importe quel grand nombre, et je peux faire plus, en y ajoutant 1.

Qu'est-ce que Google?

Googol à 1 avec cent zéros derrière elle. Nous pouvons écrire googol en utilisant des exposants, en disant, ce googol il 10 ^ 100.

Plus grand numéro nommé, nous savons, au googolplex, dix au googol, C'est (10) ^ (10 ^ 100). Il est écrit comme un, suivi de zéros googol.

En plus, il y a googolplex, c'est-à-dire un, suivi de zéros googol. Googolplex est en fait un numéro inutile pour la communauté scientifique, car il dépasse le nombre de particules dans l'univers.

Qu'appelle-t-on grands nombres?

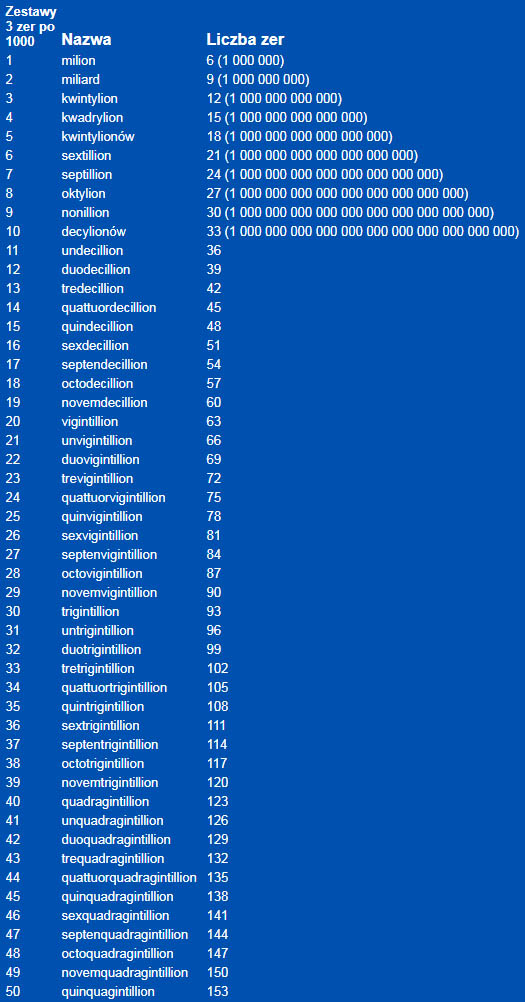
Il y a un différend à ce sujet en anglais, comment appeler de grands numéros. Il existe deux systèmes, américain et anglais:

Américain:                    Nombre de puissance

Mille                             1,000        10^ 3
Million                          1,000,000        10^6
Milliard                      1,000,000,000        10^9
Mille milliards                 1,000,000,000,000       10^ 12
Quadrillion          1,000,000,000,000,000       10^15
Quintillions      1,000,000,000,000,000,000       10^18


Anglais:            

Mille                             1,000        10^3
Million                          1,000,000        10^6
Mille million             1,000,000,000        10^9
Milliard                  1,000,000,000,000       10^12
Mille milliards     1,000,000,000,000,000       10^15
Mille milliards         1,000,000,000,000,000,000       10^ 18

Nombre le plus élevé. Le plus grand nombre nommé utilisé lexicographiquement dans le système des puissances successives des dizaines est le centillion, C'est 1, suivie par 303 zéro, C'est 10³⁰³ dans le système américain. Le plus grand nombre nommé en dehors de la notation décimale est l'asankhyeya bouddhiste, qui est égal à 10¹⁴⁰ le 100 dans l'objet-kwryrylionów.

Nombre 10¹⁰⁰ (10 duorigintillion) est étiqueté comme Googol, terme développé par le Dr Edward Kasner des États-Unis (zm. 1955). Dix élevé au pouvoir de Googol est décrit comme Googolplex. Un certain concept de l'ampleur de tels nombres peut être obtenu, en disant, que le nombre d'atomes dans certains modèles de l'univers observable ne dépasse probablement pas 10⁸⁵.

Le nombre le plus élevé jamais utilisé dans une preuve mathématique est la valeur seuil publiée dans 1977 année et connu sous le nom de nombre de Graham. S'applique aux hypercubes bichromatiques et est inexprimable sans une notation spéciale "flèche", compilé par Knuth v 1976 année. Prolongé à 64 couches.

Numéro record de Graham Gardner::
M* ≤ 3→3→(..4.) {#64#}
< 2→3→65→2 == 2→3→(..8.) {#64#}

Le numéro d'origine de Graham était plus petit:
N* ≤ 2→3→(..12.) {#7#}
< 4→2→8→2 < 2→3→9→2

le numéro de Graham c'est un nombre énorme, qui se pose comme la limite supérieure de la réponse à un problème dans le domaine mathématique de la théorie de Ramsey . Le nom vient du nom du mathématicien Ronald Graham , qui a utilisé le nombre dans des conversations avec l'écrivain de vulgarisation scientifique Martin Gardner comme explication simpliste des limites supérieures du problème, sur lequel il travaillait. O 1977 Gardner a décrit ce nombre dans Scientifique américain , en le présentant à un large public. Au moment de son introduction, c'était le plus grand entier positif spécifique, jamais utilisé dans une preuve mathématique publiée.

Le nombre de Graham est beaucoup plus grand que beaucoup d'autres grands nombres, comme le nombre de Skewes et le nombre de Moser , qui sont à leur tour beaucoup plus gros que googolplex . Comme avec ces, c'est tellement grand, que l'univers observable est beaucoup trop petit, pour accueillir la représentation numérique habituelle du nombre de Graham, en supposant, que chaque chiffre occupe un volume de Planck , peut-être le plus petit espace mesurable. Mais même le nombre de chiffres dans cette représentation numérique du nombre de Graham serait un si grand nombre en soi, que sa représentation numérique ne peut pas être représentée dans l'univers observable. Même pas le nombre de chiffres ça ne peut pas nombre – et ainsi de suite, bien au-delà du nombre total de volumes de Planck dans l'univers observable. Donc, le nombre de Graham ne peut même pas être exprimé en termes de tours de puissance de cette forme.

Cependant, le nombre de Graham peut être donné de manière unique par des formules récursives calculables utilisant la notation flèche vers le haut de Knuth ou l'équivalent, comme Graham l'a fait. Parce qu'il existe une formule récursive, qui le définit, il est beaucoup plus petit que le nombre typique de castors mobiles . Même si c'est trop gros, afin qu'il puisse être calculé dans son intégralité, la séquence de chiffres d'un nombre de Graham peut être calculée explicitement à l'aide d'algorithmes simples.