Jaka jest największa liczba? Co to jest googol? Jak nazywamy duże liczby? Co to jest nieskończoność?
Jaka jest największa liczba?
Nie ma największej liczby! Czemu? Cóż, 1 000 000 000 (1 miliard) nie może być największą liczbą, ponieważ 1 miliard + 1 jest większa – ale to prawda dla każdej wybranej liczby. Możesz wybrać dowolną dużą liczbę, a ja mogę zrobić większą, dodając do niej 1.
Co to jest googol?
Googol to 1 ze stoma zerami za nią. Możemy napisać googol przy użyciu wykładników, mówiąc, że googol to 10 ^ 100.
Największa nazwana liczba, jaką znamy, to googolplex, dziesięć do potęgi googol, czyli (10) ^ (10 ^ 100). Jest to zapisane jako jedynka, po której następują zera googol.
Poza tym jest googolplex, czyli jedynka, po której następują zera googol. Googolplex jest w rzeczywistości bezużyteczną liczbą dla społeczności naukowej, ponieważ przekracza liczbę cząstek we wszechświecie.
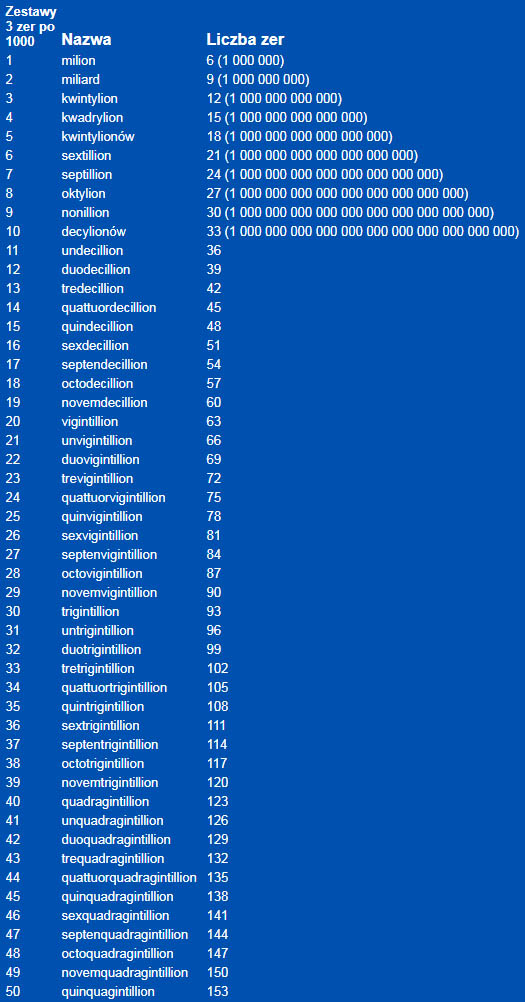
Jak nazywamy duże liczby?
W języku angielskim istnieje spór co do tego, jak nazywać duże liczby. Istnieją dwa systemy, amerykański i angielski:
Najwyższa liczba. Najwyższą nazwaną liczbą przyjętą leksykograficznie w systemie kolejnych potęg dziesiątek jest centylion, czyli 1, po którym następuje 303 zera, czyli 10303 w systemie amerykańskim. Najwyższą nazwaną liczbą poza zapisem dziesiętnym jest buddyjska asankhyeya, która jest równa 10140 lub 100 kwinto-kwadrylionów.
Liczba 10100 (10 duotrigintillion) jest oznaczona jako Googol, termin opracowany przez dr Edwarda Kasner z USA (zm. 1955). Dziesięć podniesionych do potęgi Googola jest opisywane jako Googolplex. Pewną koncepcję wielkości takich liczb można uzyskać, mówiąc, że liczba atomów w niektórych modelach obserwowalnego wszechświata prawdopodobnie nie przekracza 1085.
Najwyższa liczba kiedykolwiek użyta w dowodzie matematycznym to wartość graniczna opublikowana w 1977 roku i znana jako liczba Grahama. Dotyczy dwuchromatycznych hipersześcianów i jest niewyrażalna bez specjalnej notacji „strzałki”, opracowanej przez Knutha w 1976 roku. Rozszerzona do 64 warstw.
Oryginalna liczba Grahama była mniejsza: N* ≤ 2→3→(..12.) {#7#} < 4→2→8→2 < 2→3→9→2
Liczba Grahama to ogromna liczba, która powstaje jako górna granica odpowiedzi na problem z matematycznej dziedziny teorii Ramseya . Nazwa pochodzi od nazwiska matematyka Ronalda Grahama , który użył liczby w rozmowach z pisarzem popularnonaukowym Martinem Gardnerem jako uproszczone wyjaśnienie górnych granic problemu, nad którym pracował. W 1977 roku Gardner opisał tę liczbę w Scientific American , przedstawiając ją szerokiej publiczności. W momencie jego wprowadzenia była to największa specyficzna dodatnia liczba całkowita, jaka kiedykolwiek została użyta w opublikowanym dowodzie matematycznym.
Liczba Grahama jest znacznie większa niż wiele innych dużych liczb, takich jak liczba Skewesa i liczba Mosera , z których oba są z kolei znacznie większe niż googolplex . Podobnie jak w przypadku tych, jest tak duży, że obserwowalny wszechświat jest o wiele za mały, aby pomieścić zwykłą cyfrową reprezentację liczby Grahama, zakładając, że każda cyfra zajmuje jedną objętość Plancka , prawdopodobnie najmniejszą mierzalną przestrzeń. Ale nawet liczba cyfr w tej cyfrowej reprezentacji liczby Grahama byłaby sama w sobie liczbą tak dużą, że jej cyfrowej reprezentacji nie można przedstawić w obserwowalnym wszechświecie. Ani nawet liczba cyfr tego nie może liczba – i tak dalej, wielokrotnie znacznie przekraczając całkowitą liczbę tomów Plancka w obserwowalnym wszechświecie. Tak więc liczby Grahama nie można wyrazić nawet za pomocą wież mocy tej formy.
Jednak liczbę Grahama można jednoznacznie podać za pomocą obliczalnych formuł rekurencyjnych przy użyciu notacji Knutha ze strzałką w górę lub jej odpowiednika, tak jak zrobił to Graham. Ponieważ istnieje rekurencyjna formuła, która ją definiuje, jest ona znacznie mniejsza niż typowe liczby ruchliwych bobrów . Chociaż jest zbyt duża, aby można ją było obliczyć w całości, sekwencja cyfr liczby Grahama może być obliczona jawnie za pomocą prostych algorytmów.
