die größte Zahl
Was ist die größte Anzahl? Was ist Google? Wie nennen wir große Zahlen? Was ist unendlich?
Was ist die größte Anzahl?
Es gibt nicht die größte Anzahl! Warum? Also, 1 000 000 000 (1 Milliarde) kann nicht die größte Zahl sein, Weil 1 Milliarde + 1 ist größer – aber es gilt für jede Zahl, die Sie wählen. Sie können eine beliebige große Anzahl auswählen, und ich kann mehr tun, dazu hinzufügen 1.

Was ist Google?
Googol zu 1 mit hundert Nullen hinter ihr. Wir können Googol mit Exponenten schreiben, Sprichwort, das googol es 10 ^ 100.
Größte benannte Nummer, wir wissen, zu googolplex, zehn zum googol, Das ist (10) ^ (10 ^ 100). Es wird als eins geschrieben, gefolgt von Googol-Nullen.
Außerdem gibt es Googolplex, das heißt, einer, gefolgt von Googol-Nullen. Googolplex ist eigentlich eine nutzlose Zahl für die wissenschaftliche Gemeinschaft, weil es die Anzahl der Teilchen im Universum überschreitet.
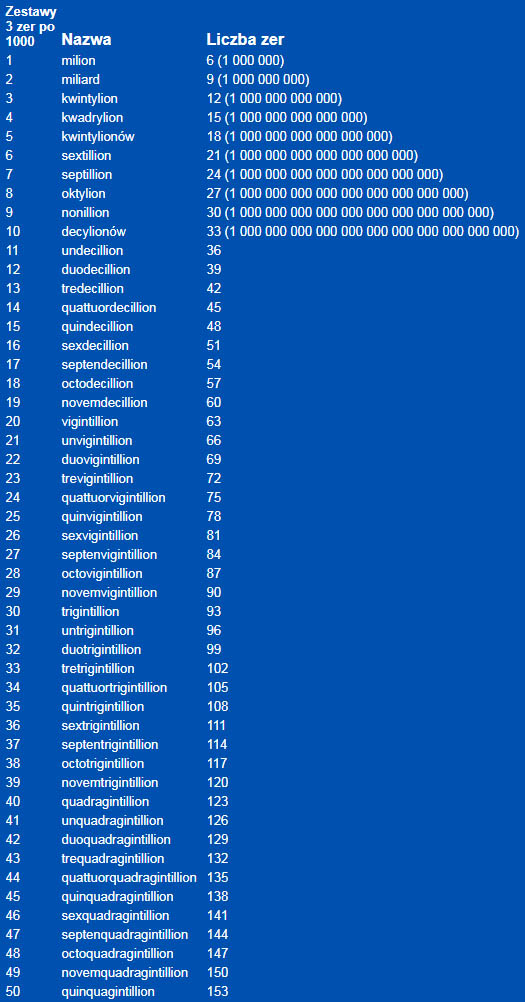
Wie nennen wir große Zahlen?
Es gibt einen Streit darüber auf Englisch, wie man große Nummern anruft. Es gibt zwei Systeme, Amerikanisch und Englisch:
amerikanisch: Potenznummer Tausend 1,000 10^3 Million 1,000,000 10^ 6 Milliarde 1,000,000,000 10^ 9 Billion 1,000,000,000,000 10^ 12 Billiarde 1,000,000,000,000,000 10^ 15 Trillion 1,000,000,000,000,000,000 10^ 18 Englisch: Tausend 1,000 10^3 Million 1,000,000 10^ 6 Tausend Millionen 1,000,000,000 10^ 9 Milliarde 1,000,000,000,000 10^ 12 Tausend Milliarden 1,000,000,000,000,000 10^ 15 Billion 1,000,000,000,000,000,000 10^ 18
Höchste Zahl. Die höchste benannte Zahl, die lexikographisch im System aufeinanderfolgender Zehnerpotenzen verwendet wird, ist der Centillion, Das ist 1, gefolgt von 303 Null, Das ist 10303 im amerikanischen System. Die höchste benannte Zahl außerhalb der Dezimalschreibweise ist das buddhistische Asankhyeya, das ist gleich 10140 Die 100 im Objekt-kwryrylionów.
Nummer 10100 (10 Duotrigintillion) ist als Googol gekennzeichnet, Begriff entwickelt von Dr. Edward Kasner aus den USA (d. 1955). Zehn, die zur Macht von Googol erhoben wurden, werden als Googolplex bezeichnet. Ein bestimmtes Konzept der Größe solcher Zahlen kann erhalten werden, Sprichwort, dass die Anzahl der Atome in einigen Modellen des beobachtbaren Universums wahrscheinlich nicht überschreitet 1085.
Die höchste Zahl, die jemals in einem mathematischen Beweis verwendet wurde, ist der in 1977 Jahr und bekannt als Grahams Nummer. Gilt für bichromatische Hyperwürfel und ist ohne spezielle "Pfeil" -Notation nicht auszudrücken, zusammengestellt von Knuth v 1976 Jahr. Erweitert um 64 Schichten.
Graham Gardners Rekordnummer::
M * ≤ 3→3→(..4.) {#64#}
< 2→ 3 →65→ 2 == 2 → 3 →(..8.) {#64#}
Grahams ursprüngliche Nummer war kleiner:
N * ≤ 2→3→(..12.) {#7#}
< 4→2→8→2 < 2→ 3 →9→ 2
Grahams Nummer das ist eine riesige Zahl, Dies ergibt sich als Obergrenze der Antwort auf ein Problem im mathematischen Bereich der Ramsey-Theorie . Der Name stammt vom Namen des Mathematikers Ronald Graham , der die Zahl in Gesprächen mit dem populärwissenschaftlichen Autor Martin Gardner als vereinfachte Erklärung der oberen Grenzen des Problems verwendete, woran er arbeitete. In 1977 Gardner beschrieb diese Nummer in Wissenschaftlicher Amerikaner , indem wir es einem breiten Publikum vorstellen. Zum Zeitpunkt seiner Einführung war es die größte spezifische positive ganze Zahl, jemals in einem veröffentlichten mathematischen Beweis verwendet.
Grahams Zahl ist viel größer als viele andere große Zahlen, wie Skewes 'Nummer und Mosers Nummer , Beide sind wiederum viel größer als Googolplex . Wie bei diesen, Es ist so groß, dass das beobachtbare Universum viel zu klein ist, die übliche digitale Darstellung einer Graham-Nummer enthalten, unter der Annahme, dass jede Ziffer ein Planck-Volumen belegt , möglicherweise der kleinste messbare Raum. Aber selbst die Anzahl der Ziffern in dieser digitalen Darstellung von Grahams Nummer wäre an sich schon eine so große Zahl, dass seine digitale Darstellung nicht im beobachtbaren Universum dargestellt werden kann. Nicht einmal die Anzahl der Ziffern es kann nicht Nummer – usw, um ein Vielfaches über der Gesamtzahl der Planck-Volumina im beobachtbaren Universum. Grahams Zahl kann also nicht einmal in Form der Krafttürme dieser Form ausgedrückt werden.
Die Graham-Zahl kann jedoch eindeutig durch berechenbare rekursive Formeln unter Verwendung der Knuth-Notation mit einem Aufwärtspfeil oder einem Äquivalent angegeben werden, wie Graham es tat. Weil es eine rekursive Formel gibt, was es definiert, es ist viel kleiner als die typische Anzahl von mobilen Bibern . Obwohl es zu groß ist, damit es vollständig berechnet werden kann, Die Ziffernfolge einer Graham-Zahl kann mit einfachen Algorithmen explizit berechnet werden.










